Why quants play credit card roulette and sell insurance for free
How a quant-favorite dinner game seems like gambling but is actually underwriting
What is Credit Card Roulette?
One of the weirder habits of quants is that they like to play credit card roulette. The gist of the game is this:
Imagine you are eating at a restaurant with your fellow quantitatives. The check arrives and it comes to $B among N of you. You could split the check equally but that wouldn't be fun. Instead all the (Chase Sapphire Reserve) credit cards get dropped in the middle and one is pulled out at random. That poor soul must pay the entire credit card bill himself.
It’s a strange game. You might wonder why quants seem to enjoy playing it.
In expectation, paying for the check this way is equivalent to splitting it equally. So, on average, no-one is worse off than if they didn’t play this game.
Maybe this is intuitive. Here's the quick maths in case it’s not:
The variance is different, though.
Before that let me quickly gesture at what variance is.
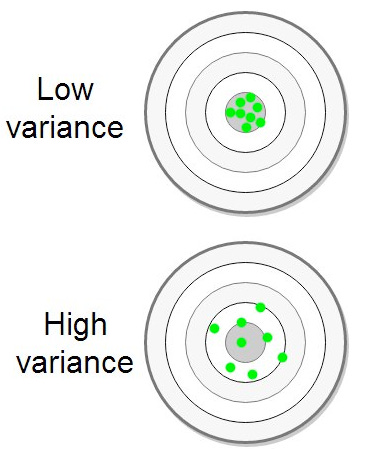
Intuitively variance is about the spread of outcomes. Below are two dartboards with a low variance set of throws and a high variance set of throws. Both are roughly centered around the middle of the dartboard but the higher variance thrower has more spread in their throws.
Ok, so I said the variance is different. But what is the variance in each case?
If we don’t play the game I always pay $B/N. There is no spread in my outcomes so my variance is 0. Like an even more clustered version of the top dartboard.
If we do play the game, I have a variety of outcomes. Below is the math for the variance which isn’t super important in and of itself but my non-compete ends soon and I need to keep up my quant credentials.
The point here is assuming you’re not dining solo (N>1) and your food costs money (B>0), your variance when playing this game is always greater than 0.
Quants care about EV much more than variance
Quants seem to like this game because it adds variance without changing the expected value (EV). They spend their whole lives chasing positive EV outcomes without much thought for variance so a 0 EV game is fine for them to play.
In fact this is the safest game to play with other quants who are constantly on the lookout for positive EV games and bets to make with you.
Most famously, this particular way of thinking about the world applied to Sam Bankman-Fried when he worked at Jane Street. [1]
Positive EV is literally the alpha or the edge. Quants care about alpha. That’s the only thing that matters to so many of them [2] that they can be earning north of six figures and live in rooms that look like this:
And this is all well and good but here’s the rub: playing a game that doesn’t change your EV but adds variance is literally the opposite of what people want from large parts of the finance industry.
Isn’t that the opposite of insurance?
Quants inhabit a mysterious part of finance. Who are they, why do they play these games, why do they all have international math olympiad medals, how can I too work for Citadel? In their own weird way, quants are sexy.
Insurance is not sexy. It is nonetheless extremely important in the world of finance. And it’s conceptually neat too.
Take car insurance. You can pay an insurer each month, and if something bad happens to your car or because of your car, you are financially covered by that insurer.
The exact average won’t always apply to one person; the insurer could lose money from the first customer they have. You could, for example, accidentally fire your shotgun into your own car.
Instead the insurer sells a similar product to a lot of people. Rather than hoping for a lucky flip of the coin for one person, they can make money in a more predictable manner. Car crashes are mostly uncorrelated with each other.
There are obviously more details and weird incentives in any given insurance policy, but the long and short of it is this: you can pay now to reduce your variance in the future.
On average you should expect to lose money when buying insurance. Otherwise, why would the company sell it to you? But in the case of something really bad happening, like a mattress flying off the back of your car into someone else’s car, insurance is there just in case.
Putting it all together
So why is there such a big difference between these two groups of people?
Ordinary people who want to decrease their future variance so much they’re willing to pay for it and buy insurance, and
Quants who seemingly want to increase their variance?
A few thoughts on this.
Quants get bored at restaurants. Credit card roulette isn’t the only game quants play at restaurants [3]. Playing a 0 EV gambling game is a way to pass the time.
The scales are wildly different. If the restaurant bill was for $100k quants and totaled $10m they would be less inclined to play the game. The downside risk would be ruinous for most.
The richer you are the less it matters to you losing some amount of money. Losing $500 when you have $500k in the bank is very different to losing $500 when you have $400 in the bank. Your risk preferences are a function of your wealth.
High frequency trading quants are used to acting like the house. I’ll come back to this in a minute but first:
Isn’t it just gambling?
When I was 10 years old I lost £20 to Daniel Cheung while playing poker. £20 is literally all of the money to a 10 year old. It was so scarring that I haven’t bet money on anything since.
But other people love to gamble. They knowingly play a negative EV game for the potential of a huge payout. This is, like insurance, a transfer of tail risk for a price. Except this tail risk is in the other direction: as a casino your customers are looking for positive upside risk and are willing to pay you for it.
In both gambling and insurance, the positive EV side of the trade takes on the downside risk in exchange for positive EV
insurance will cover liabilities after a car crash
a casino will pay out any large pay-day
And their task is to spread that across so many clients that they don’t get wiped out by too large a downside risk event occurring [4].
Quants play like the house
By playing credit card roulette and the potentially large downside that comes with it, the quant’s payoff is less like a gambler’s and more like that of a casino or an insurance company: the quant takes on the large downside risk for… no increase in their EV.
We know people are willing to pay to remove downside risk and yet the quant does it for free. They’re acting as an insurance provider to every other quant at the table. But so is every other quant.
Imagine a different game, let’s call it “The Quant Lottery”, where everyone puts in $100 and a randomly chosen person gets the winnings. This has a payoff much more like gambling than credit card roulette does. This game is sort of the opposite of credit card roulette where everyone takes out $100 (eats a meal) and a randomly chosen person has to pay the debt while everyone else gets a free meal.
Why don’t quants play this game and instead play credit card roulette?
High frequency trading quants are trained to think like the house not like the gambler. Upside for free seems like a trick to them.
Quants are shielded from downside risk via their companies. The median outcome of the credit card lottery game is that you get a free meal. Quants are often paid on the realization of their strategies not the expectation of them. If most of the time you have a winning strategy, then in most versions of the world you have a good bonus. If sometimes your strategy blows up, then your worst case is you’ll be fired. You don’t have skin in the game for the true downsides of your strategies.
So quants are just underwriters?
A few lessons here:
Quants think they’re playing credit card roulette, but really they’re underwriting someone else’s dinner.
Don’t take bets suggested to you by quants.
Car insurance is a good idea.
If you must gamble, don’t play poker with Daniel Cheung.
I lost credit card roulette recently and I’m still on my non-compete. This piece has been brought to you by the need to gain more subs to pay off the debt incurred.
[1] Matt Levine commented a couple years ago:
Jane Street, after all, is not betting its entire bankroll on any one intern, or trader, or trading team. Jane Street has a diversified portfolio of (it hopes) independent positive-expected-value bets created by different traders. If one trader bets her whole bankroll on a trade that is good in expectation, and it blows up and she loses everything, that’s fine for Jane Street: They have lots more traders doing bets like that, and in the long run the good bets will make more than the bad ones lose.
In this description of Jane Street the quants can focus on making positive EV bets and the risk manager/portfolio optimizer/father figure cares about the risk.
[2] Apart from that one guy at Two Sigma who maybe changed the risk parameters of a few of Two Sigma’s models and netted himself $23m before getting accused of rigging the models to be higher risk.)
[3] For a quick teaser: the market making game involves going around the dinner table with quants successively stating smaller and smaller confidence intervals for what they think the final check value will be. Eventually a quant gives a range (eg $7) so narrow no-one else can go smaller. That quant then shares their actual numbers (eg $90-$97) and the rest of the group bets over or under the interval. If the final check comes inside the interval then the market maker wins, otherwise whoever bet the right way wins.
[4] I’ve explained this a number of times in this piece but it’s important!
The best rationalization I've heard for gambling was by Aaron Brown IIRC. Taking the old American West as an example, he said gambling provided utility by allowing capital to be concentrated. Normally a bank or VC would do this, but in the old West, banks could be robbed and no one had much insight on people's business acumen since everyone was transient. Capital formation was needed to do large projects, for example setting up a general store or mine. No one individually could do much besides hold their few coins, but if they won the rest of the town's money then they could build something bigger, benefiting everyone.